|
|
写在前面
做的东西不是热门,很多东西网上找资料也不是很方便,想了好久想把自己会的东西写成文字,也许能够帮到一些有缘人。
第一篇文字写什么呢?思来想去,还是确定这个题目。
引言
渗透系数(K)作为最为重要的水文地质参数,具有强弱不均的空间变异性。渗透系数的均质性假设和参数分区方法都有着明显的局限性。
含水层的渗透系数通常可视为一个在空间上存在相关关系的随机场,并且通常服从对数正态分布,因此对其进行对数化处理后可将其视为高斯随机场(这是应用中最常见的情形)。
对于高斯渗透系数随机场(K field),不仅需要随机变量K的均值和方差,还需要得到随机变量之间在空间上的相关关系。通常可以利用变差函数以及协方差函数来描述变量在空间上的相关关系。均值(mean)和方差(variance)这个很简单,就不说了,下面先说变差函数(semi-variogram,或者variogram)。
变差函数
先抄个定义。
定义
变差函数:空间变量Z(x)和Z(x+h)之差( Z(x)-Z(x+h) )的方差的一半,定义为Z(x)的变差函数
V(x,h)=\frac{1}{2}Var[Z(x)-Z(x+h)] , 其中,h 为滞后距
具体来说,若相同滞后距 h 的空间点对为N 组,则: v(h)=\frac{1}{2N}\sum_{i=1}^{N}{[Z(x_i)-Z(x_i+h)]^2}
以一维情形为例说明,某钻孔孔隙度数据(以1m 间距进行测定,单位:%), \theta=[7.25, 8.00,6.25,4.29,5.98,10.23,12.11,4.20,5.44,6.23] ,
则 h = 1对应的空间数据点对 [Z(x_i), Z(x_i+h)] :[(7.25,8.00), (8.00,6.25),(6.25,4.29),(4.29,5.98),(5.98,10.23),(10.23,12.11),(12.11,4.20),(4.20,5.44),(5.44,6.23)]
容易计算得到: v(h=1)=5.37 ,同样可以得到 v(h=2)=12.26
需要注意的是:在实际问题中,考虑到空间异性特征,就需要计算不同方向的变差函数值,这时候的滞后距h就是沿着某方向的移动距离。
变差函数类型(常用)[1]
球型(spherical)
\gamma(h)=C[\frac{3}{2}\frac{h}{a}-\frac{1}{2}(\frac{h}{a})^3]
指数型(exponential)
\gamma(h)=C[1-e^{-3(\frac{h}{a})}]
高斯型(gaussian)
\gamma(h)=C[1-e^{-3(\frac{h}{a})^2}]
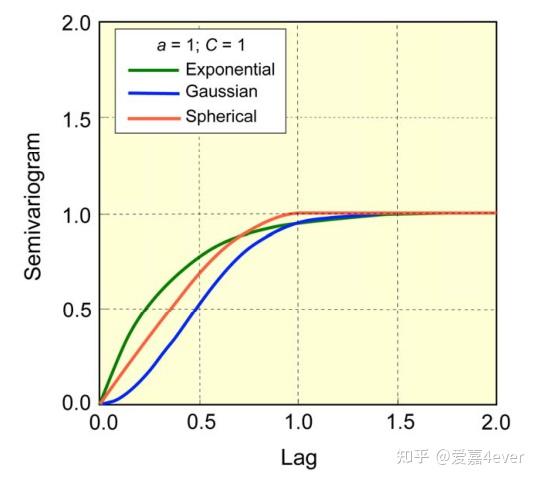
图1 常用的变差函数类型
地质统计学建模
上面简单介绍了变差函数,有了这个工具,下面可以说说如何利用地质统计学刻画渗透系数场。在地质统计学建模方法中,包括确定性建模和随机建模。
确定性建模
确定性建模就是利用已有取样点(采样点)资料给出确定性的预测(估计)结果。最具有代表性的方法就是kriging方法。
建模步骤:(1)计算实验变差函数(图2b的黑点);(2)选择合适的变差函数类型进行拟合(图2b的蓝色线);(3)利用得到的变差函数进行kriging插值(图2c)。
需要注意的是,大多数具有空间分析功能的商业软件都可以直接根据空间数据(图2a)直接得到kriging插值图(图2c),采用的是默认变差函数。对于一般性问题,这种处理是可以的。对于空间分析要求较高的问题,我这里还是建议用推荐的建模步骤。
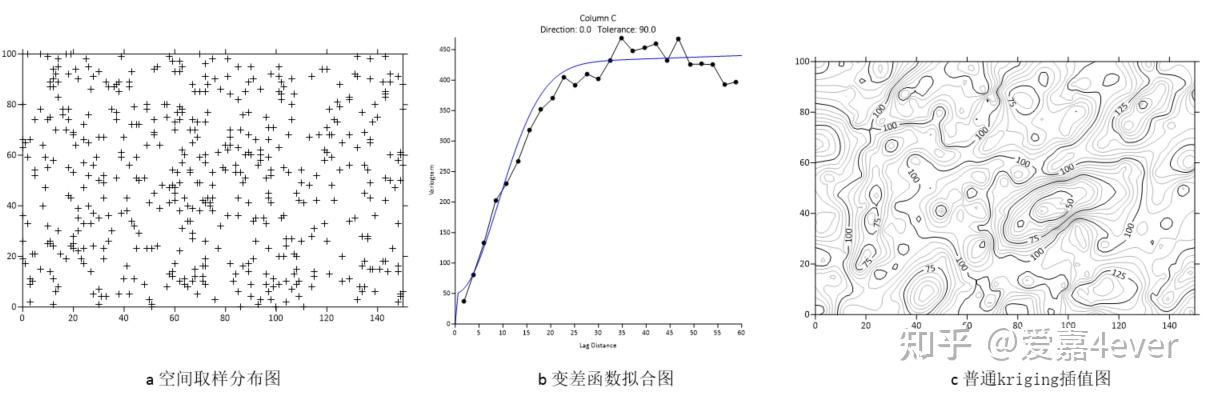
图2 确定性建模预测(Kriging方法)
随机建模
对应于地下水领域的不确定性模拟方法,对于地下水计算问题中最重要的参数(渗透系数)同样需要刻画其不确定性(随机特性)。下面就利用地质统计学的随机建模方法进行渗透系数场的刻画,这里我们选用顺序高斯模拟(Sequential Gaussian Simualation,SGS)。
建模步骤:(1)计算实验变差函数;(2)选择合适的变差函数类型进行拟合;(3)进行SGS随机建模。
前两步与确定性建模方法完全一样,考虑到后续希望将渗透系数随机模拟与地下水逆问题相结合,因而这里我们采用计算效率颇高的SGS开源程序(matlab)[2]。
上例子:
某含水层为二维非均质各向同性的承压含水层(32m × 20m),用边长为 0.5 m的正方形网格将区域剖分为65行41列的有限差分网格。含水层渗透系数场满足均值为3.0,方差为 1.0的对数正态分布。在x和y方向的相关长度分别为9 m和6 m,变差函数为指数型。
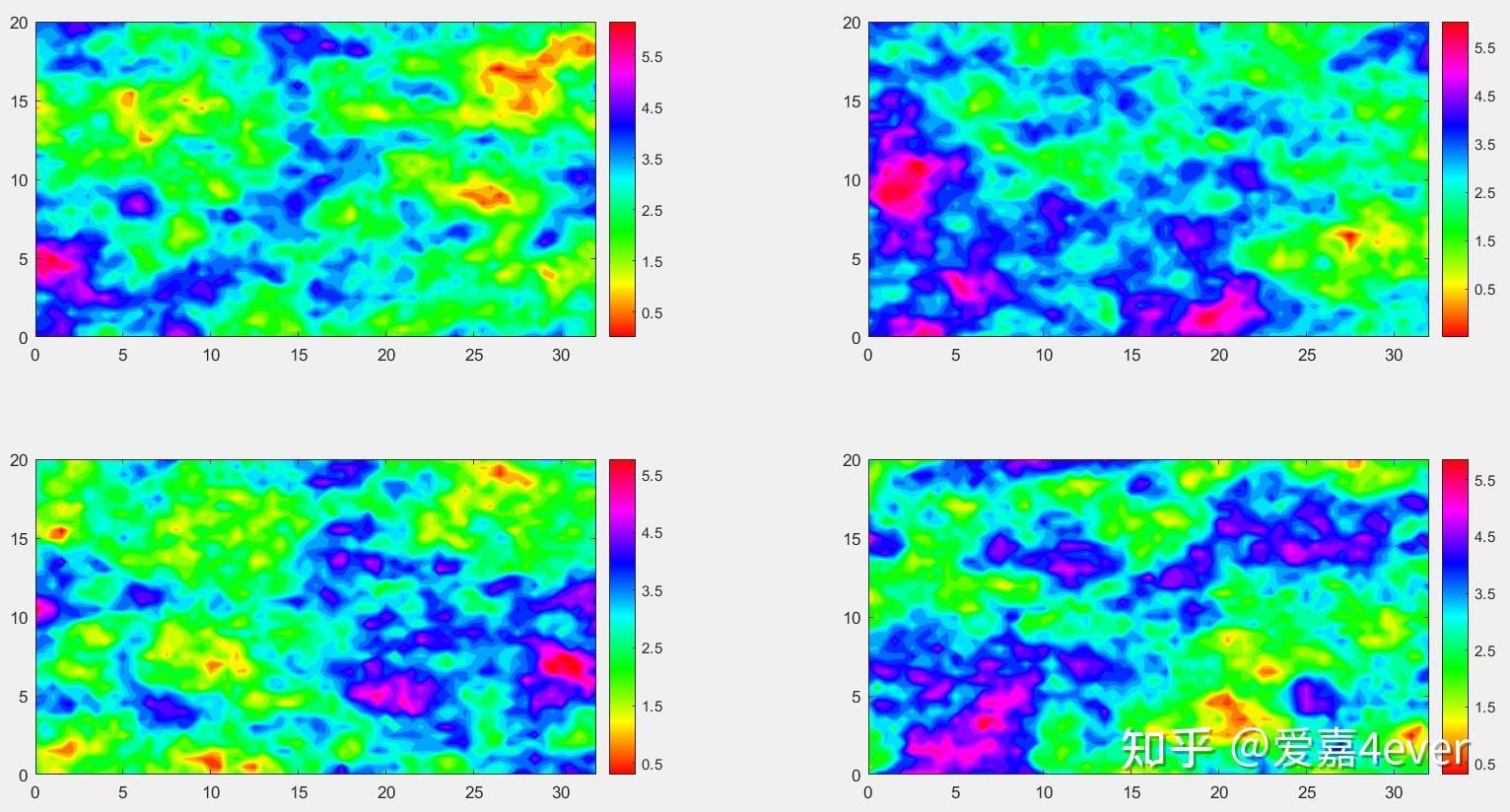
图3 利用SGS得到的10000个对数渗透系数场(随机选择4组实现展示)
%% https://rafnuss-phd.github.io/SGS/html/script_SGS
clear;clc
nx = 65; % number of cell along x
ny = 41; % number of cell along y
%m = 1; % number of realization
covar.model = 'exponential'; % type of covariance function, see functions/kriginginitiaite.m for option
covar.range0 = [18 12]; % range of covariance [y x] y理解为主方向更合适,因此需要与azimuth对应
covar.azimuth = 90; % orientation of the covariance 主变程方向0-正北(y),90-正东(x)
covar.c0 = 1; % variance
covar.alpha = 1; % parameter of covariance function (facult)
parm.saveit = false; % save in a file
parm.seed_path = 'shuffle'; % seed for the path
parm.seed_search = 'shuffle'; % seed for the search (equal distance node)
parm.seed_U = 'shuffle'; % seed of the node value sampling
parm.mg = 1 ; % multigrid vs randomized path
neigh.wradius = 3; % maximum range of neighboorhood search, factor of covar.range.
neigh.lookup = false; % lookup table.
neigh.nb = 40; % maximum number of neighborhood
method = 'trad'; % SGS method: cst_par, cst_par_cond, hybrid, varcovar
m=10000;
[Rest, t] = SGS(nx,ny,m,covar,neigh,parm, method);
Y = Rest +3.0; % Y=lnK
save Y_10000_41_65.mat Y对于初学者,利用网上学习资料更多的SGEMS是不错的选择[3],它具有可视化用户界面,matlab环境中也有mgstat程序包可供使用。
结语
其实,对于地质统计学,本人并非科班,我只是用的比较多一些。对于各种软件工具,对拟使用的方法背后的原理以及优缺点还是要清楚的,不然就“呵呵”了
这篇文章的地质统计学是基于变差函数的,也就是传统的两点地质统计学。
对于多点地质统计有兴趣的,这里也推荐下开源程序[4]。
先写这么多,直接在知乎中码字的,初体验还不错。
参考
- ^A Practical Primer on Geostatistics https://pubs.er.usgs.gov/publication/ofr20091103
- ^Sequential Gaussian Simulation for generating Gaussian fields https://rafnuss-phd.github.io/SGS/
- ^SGeMS http://sgems.sourceforge.net/
- ^G2S: The GeoStatistical Server https://gaia-unil.github.io/G2S/
|
|